Fraunhofer-Institut für Lasertechnik ILTIm einfachsten Fall kann man sich einen Resonator als allseits geschlossenen Kasten mit hoch reflektierenden Wänden vorstellen. Da die Laserwellenlängen viel kleiner sind als ein solcher Kasten realistischerweise sein könnte, würden viele verschiedene Moden oder Eigenschwingungen angeregt (hier spielen technische Begrenzungen eine Rolle, aber insbesondere die Tatsache, daß für eine hinreichnde Verstärkung das Lasermedium ein Mindestvolumen haben muss). Die Laserstrahlung wäre dann nicht mehr gebündelt.
Optischer Resonator
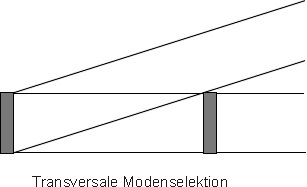
Um eine Vorzugsrichtung auszusondern, werden sogenannte offene Optische Resonatoren eingesetzt. Dabei werden zwei Spiegel parallel und auf eine gemeinsame optische Achse zentriert in einem Abstand angeordnet, der sehr viel größer ist als der Spiegeldurchmesser. Der Teil der Strahlung, der nicht nahezu parallel zur optischen Achse emittiert wird, verlässt den Optischen Resonator sehr schnell und wird nicht weiter verstärkt. Offene Optische Resonatoren wirken somit nur für die Strahlung als rückkoppelndes Element, die nahzu parallel zur optischen Achse verläuft, es wird ein bestimmter Strahlungsmode diskriminiert, alle anderen Moden werden unterdrückt (oder die meisten anderen). Das Strahlungsfeld eines Lasers besitzt keine über den Querschnitt homogene Intensitätsverteilung. Die Intensität ist transversal zur Ausbreitungsrichtung moduliert und fällt nach außen hin nicht abrupt, sondern stetig ab. Dies ist durch Beugung bedingt, ein Phänomen, daß auf die Wellennatur des Lichtes zurückzuführen ist. Intensitätsverteilungen, die sich nach einem Umlauf durch den Resonator reproduzieren, nennt man Eigenlösungen oder Eigenmoden des Optischen Resonators. Näherungsweise können diese Eigenmoden in kartesischen Koordinaten durch die Gauß-Hermite'schen Funktionen bzw. in Zylinderkoordinaten durch Gauß-Laguerre'sche Funktionen beschrieben werden. Im allgemeinen müssen zur Berechnung von Laserstrahlungsmoden aber numerische Methoden eingesetzt werden.
Die Strahlung eines Lasers wird innerhalb des optischen Resonators hin - und her reflektiert. Dabei überlagern sich Teilwellen vieler Umläufe. Wenn die Wellenlänge des Strahlungsfeldes ein Vielfaches des doppelten Spiegelabstandes beträgt, überlagern sich die Teilwellen konstruktiv, andernfalls destruktiv. Dies führt zu einer Wellenlängenselektion, der Laserresonator schränkt somit nicht nur die mögliche Ausbreitungsrichtung, sondern auch die Frequenz des Laserlichtes ein. Zusätzlich zu diesem frequenzbegrenzenden Effekt des Resonators sorgt die nichtlineare Wechselwirkung des Laserstrahlungsfeldes mit dem aktiven Medium für eine weitere Verringerung der Bandbreite. In hochstabilen Lasern können Bandbreiten von unter 1 Hz erreicht werden (bei einer Mittenfrequenz von etwa 5 1014 Hz).
Einer der Spiegel weist im allgemeinen einen sehr hohen Reflexionsgrad auf, während der andere Spiegel eine endliche Reflektivität besitzt und einen Teil der Strahlung durchlässt. Die Transmission dieses Auskoppelspiegels kann je nach Lasertyp weniger als 1% bis zu 70 - 80 % betragen. Der optimale Wert für maximale Leistungsauskopplung hängt von der Verstärkung des aktiven Lasermediums und den Verlusten durch Absorption, Streuung und Beugung ab. Bei zu großer Transmission ist die Intensität des Strahlungsfeldes im Resonator und damit im aktiven Volumen zu gering, die spontane Absorption und andere Prozesse, die zu einer Abregung des oberen Laserniveaus führen, überwiegen die stimulierte Emission. Bei zu geringer Transmission wird das Strahlungsfeld sehr oft hin - und her reflektiert. Da bei jedem Umlauf Strahlung durch Absorption z.B. an Verunreingungen, Streuung und insbesondere Beugung verloren geht, steigen die Gesamtverluste mit der Zahl der Umläufe an (ein Teil der Laserstrahlung trifft jeweils nicht auf die Spiegel, sondern außerhalb der Spiegelfläche auf und ist damit verloren). Je nach Verstärkung und Verlusten ergibt sich somit ein optimaler Wert für die Transmission.